|
|
 发表于 2023-3-25 19:57:59
|
显示全部楼层
发表于 2023-3-25 19:57:59
|
显示全部楼层
First Normal Form
- 一个关系模式R的所有属性的域都是原子的(该域的元素是不可分的单元),比如CS00123就不是
- 反例
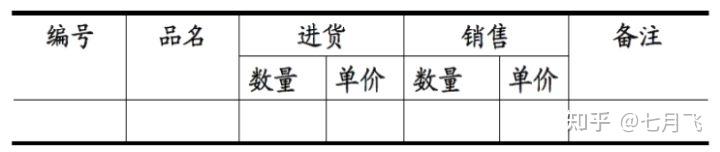
应该为

Functional Dependency
- \alpha \&\beta 是属性集
- 满足函数依赖 \alpha \rightarrow \beta 的条件:对实例中所有的元组对 t_1 和 t_2 ,若 t_1[\alpha]=t_2[\alpha] ,则 t_1[\beta]=t_2[\beta]
- 如果函数依赖 K\rightarrow R 在 r(R) 上成立,则 K 是 r(R) 的一个super key
- 如果 K 是candidate key,当且仅当 K\rightarrow R 成立而且不存在 a\subset K 且 a\rightarrow R 成立
- trivial平凡函数依赖: \alpha \rightarrow \beta 是平凡函数依赖,如果 \beta \subseteq \alpha (右侧是左侧子集)
- 如: ID, name \rightarrow ID , name \rightarrow name
函数依赖理论
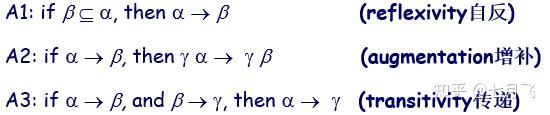
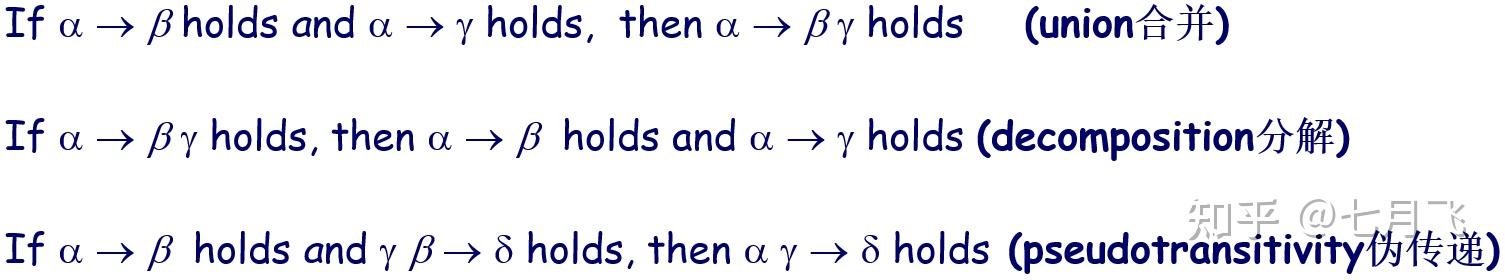

Closure
给定一个函数依赖集合 F ,能够从 F 逻辑推断的的所有函数依赖的集合称作 F 的闭包,记做 F^+

初始化时 F^+=F ,通过不断应用公理的三个规则,经产生的新的函数依赖添加到 F^+ 中,直到 F^+ 中的元素不再变化

- 如果 \alpha^+ 包含了R的所有属性,则属性集合 \alpha 是superkey。
- 如果是superkey,且 \alpha 的子集没有superkey,则是candidate key
- 如果 \beta \subseteq \alpha^+ 则函数依赖 \alpha \rightarrow \beta 成立
- 对R中的每一个属性 \gamma ,计算 \gamma^+ ,然后对于属性闭包中的每一个元素 S ,输出函数依赖 \gamma \rightarrow S
Canonical Cover 正则覆盖
- 无关属性:去除函数依赖中的一个属性,不改变函数依赖集的闭包,则是无关的extraneous。以 \alpha \rightarrow \beta 为例
- \alpha 中的无关属性A:
- F 逻辑蕴含 (F - \{\alpha \rightarrow \beta\}) \cup \{(\alpha - A)\rightarrow \beta\}
- 检测:计算 (\alpha - A)^+ ,如果包含 \beta ,则 A 是无关属性
- \beta 中的无关属性 A :
- F 逻辑蕴含 (F - \{\alpha \rightarrow \beta\}) \cup \{\alpha\rightarrow (\beta-A)\}
- 检测:利用上面的函数依赖 F' 计算 \alpha^+ ,如果包含 A 则 A 是无关属性
- 例如
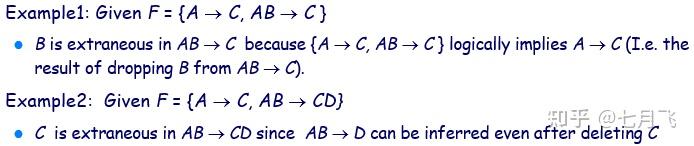
- 正则覆盖:函数依赖集合F的正则覆盖 F_c 与 F 等价(两者互相逻辑蕴含)
- 且 F_c 不包含无关属性
- F_c 中函数依赖的左侧是是唯一的( F_c 中不存在两个依赖 \alpha_1 \rightarrow \beta_1 和 \alpha_2 \rightarrow \beta_2 满足 \alpha_1=\alpha_2 ,不会一个函数依赖集合去决定多个 \beta )

例:

Lossless-join Decomposition
- R_1 和 R_2 是 R 的无损连接分解,但且仅当以下两个函数依赖之一属于 F^+
- R_1 \cap R_2 \rightarrow R_1
- R_1 \cap R_2 \rightarrow R_2
- 即, R_1 \cap R_2 是 R_1 或 R_2 的superkey
- 就是拆开后再join不会数据不会变多
- 例如

Dependency Preservation
- 依赖保持:令F是关系模式R上的一个函数依赖集,R_1,R_2...R_n为R的一个分解,F_i是只包含R_i属性的函数依赖集合
- 如果 (F_1\cup F_2 \cup ... \cup F_n)^+ = F^+ ,这个分解是依赖保持的
- 检测:

Boyce-Codd Normal Form
- 一个关系模式 R 在给定的函数依赖集合 F 下,符合BCNF的条件是:对于 F^+ 中所有的函数依赖 \alpha \rightarrow \beta ,其中 \alpha \subseteq R 且 \beta \subseteq R ,以下至少有一项成立:
- \alpha \rightarrow \beta 是平凡函数依赖
- \alpha 是 R 的一个super key
- 反例
- 关系 R 的模式为 R = (A, B, C) ,函数依赖集合为 F = \{A\rightarrow B,B \rightarrow C\} ,Key = \{A\} 。不符合: B\rightarrow C 中 B 不是super key
- 分解
- 设有一个关系模式 R 和函数依赖集合 F ,其中一个函数依赖 a \rightarrow b 导致 R 不是BCNF,这时可以将 R 进行分解为两个子模式 R_1 和 R_2 :
- R_1= (a \cup b) ,R2= (R - (b - a))
- 例:某设计者设计的关系模式为instr_dept (ID, name, salary, dept_name, building, budget ),希望管理教师和院系的数据以及教师所在院系的信息。假设a= dept_name(不是key),b = building, budget, F : {dept_name --> building,budget},instr_dept不是BCNF。分解得到
- R_1 = (dept_name, building, budget), R_2 = (ID, name, salary, dept_name)
- 最优先选择 BCNF + 依赖保持。
- BCNF分解有可能会导致某些函数依赖不在一个子模式中,不能高效地检查一些函数依赖增加代价。当无法达到BCNF和依赖保持这个目标时,就考虑“弱”一点的3NF
- 检验非平凡函数依赖 \alpha \rightarrow \beta 是否违反BCNF:
- 计算 \alpha 的闭包
- 检验闭包是否包含 R 。这就是 R 的superkey
- 其实就是看函数依赖的左边是不是superkey
- 分解算法




Third Normal Form
- 3NF是BCNF的最小放宽
- 具有函数依赖集合 F 的关系模式 R 是3NF的条件:对于 F^+ 中的所有形如 a \rightarrow b 的函数依赖, a 和 b 是 R 的子集,以下条件至少成立一个:
- a \rightarrow b 是平凡函数依赖
- a 是 R 的一个superkey(满足这一条就是BCNF)
- b - a 中的每个属性 A 都包含在 R 的一个candidate key中( b-a 中的每个属性可以包含在不同的candidate key中)
- 网上:非主键列必须直接依赖于主键,不能存在传递依赖
|
|