|
|
 发表于 2022-12-1 16:43:41
|
显示全部楼层
发表于 2022-12-1 16:43:41
|
显示全部楼层
第六章 关系数据库理论
6.1 依赖
6.1.1 函数依赖
专业定义:设R(U)是一个属性集U上的关系模式,X和Y是U的子集。若对于R(U)的任意一个可能的关系r,r 中不可能存在两个元组在X上的属性值相等, 而在Y上的属性值不等, 则称“X函数确定Y”或“Y函数依赖于X”,记作X→Y。
案例演示:在关系Student(Sno, Sname, Ssex, Sage, Sdept),假设不允许重名,有:
- Sno → Sname
- Sno → Ssex
- Sno → Sage
- Sno → Sdept
- Sname → Sno
- Sname → Ssex
- Sname → Sage
- Sname → Sdept
6.1.2 平凡函数依赖
专业定义:X→Y,但Y⊆X 则称X→Y是平凡的函数依赖。
6.1.3 非平凡函数依赖
专业定义:X→Y,但Y⊈X则称X→Y是非平凡的函数依赖。
6.1.4 完全函数依赖
专业定义:

案例演示:在关系SC(Sno, Cno, Grade)中,有:

6.1.5 部分函数依赖
专业定义:
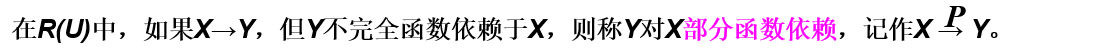
案例演示:在关系SC(Sno, Cno, Grade)中,则有:

6.1.6 传递函数依赖
专业定义:
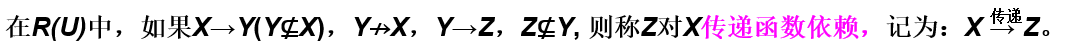
案例演示:在关系Std(Sno, Sdept, Mname)中,有:
Sno → Sdept , Sdept → Mname
6.2 码

6.3 范式
6.3.1 1NF
作为二维表,关系要符合一个最基本的条件:每个分量必须是不可分开的数据项。满足了这个条件的关系模式就属于第一范式(1NF)。
6.3.2 2NF
若关系模式R∈1NF,并且每一个非主属性都完全函数依赖于任何一个候选码,则R∈2NF。
S-L-C(Sno,Sdept,Sloc,Cno,Grade), Sloc为学生的住处,并且每个系的学生住在同一个地方。S-L-C的码为(Sno,Cno)。函数依赖有:

非主属性Sdept、Sloc并不完全依赖于码,关系模式S-L-C不属于2NF。
一个关系模式不属于2NF,会产生以下问题:
插入异常:如果插入一个新学生,但该生未选课,即该生无Cno,由于插入元组时,必须给定码值,因此插入失败。
删除异常:如果S4只选了一门课C3,现在他不再选这门课,则删除C3后,整个元组的其他信息也被删除了。
修改复杂:如果一个学生选了多门课,则Sdept,Sloc被存储了多次。如果该生转系,则需要修改所有相关的Sdept和Sloc,造成修改的复杂化。
出现这种问题的原因,例子中有两类非主属性:
一类如Grade,它对码完全函数依赖。
另一类如Sdept、Sloc,它们对码不是完全函数依赖。
解决方法:用投影分解把关系模式S-L-C分解成两个关系模式
SC(Sno,Cno,Grade)
S-L(Sno,Sdept,Sloc)
SC的码为(Sno,Cno)、SL的码为Sno,这样使得非主属性对码都是完全函数依赖了。
6.3.3 3NF

6.3.4 BCBF
BCNF(Boyce Codd Normal Form)由Boyce和Codd提出,比3NF更进了一步。通常认为BCNF是修正的第三范式,有时也称为扩充的第三范式。设关系模式R<U,F>∈1NF,若X →Y且Y ∉ X时,X必含有码,则R<U,F>∈BCNF。换言之,在关系模式R<U,F>中,如果每一个决定属性集都包含候选码,则R∈BCNF。
BCNF的关系模式所具有的性质:
所有非主属性都完全函数依赖于每个候选码
所有主属性都完全函数依赖于每个不包含它的候选码
没有任何属性完全函数依赖于非码的任何一组属性
如果一个关系数据库中的所有关系模式都属于BCNF,那么在函数依赖范畴内,它已实现了模式的彻底分解,达到了最高的规范化程度,消除了插入异常和删除异常。
考察关系模式C(Cno,Cname,Pcno),它只有一个码Cno,没有任何属性对Cno部分依赖或传递依赖,所以C∈3NF。
同时C中Cno是唯一的决定因素,所以C∈BCNF。 |
|